ทุกช่วงชีวิตของทุกคนต้องมีการตัดสินใจทางการเงิน ไม่ว่าเป็นการตัดสินใจเพื่อตัวเองหรืออนาคตของครอบครัว เช่น การตัดสินใจฝากเงิน การตัดสินใจลงทุน การตัดสินใจกู้เงิน การซื้อบ้านซื้อรถ แต่ในเมื่อไม่ว่าการฝากเงินหรือการกู้เงินต้องมีปัจจัยเรื่องระยะเวลา ดอกเบี้ย หรือแม้กระทั่งอัตราเงินเฟ้อเข้ามาเกี่ยวข้อง ซึ่งจะทำให้เงิน 1 บาทมีมูลค่าแตกต่างกันไปในแต่ละช่วงเวลา การจะประเมินผลกระทบของเงินก้อนต่างๆ ต่อสถานะการเงินและตัดสินใจได้อย่างเหมาะสมจึงไม่อาจทำได้ด้วยการดูจากตัวเลขที่ปรากฏ แต่ต้องคำนวณถึงมูลค่าที่แท้จริงของเงินก้อนนั้นๆ ด้วย
ในทางการเงิน หลักการที่ช่วยให้เห็นผลกระทบที่แท้จริงของตัวเงินที่เข้ามาหรือออกไปในระยะเวลาต่างๆ เรียกว่า “มูลค่าเงินตามเวลา” หรือ time value of money ซึ่งมีหลักการดังต่อไปนี้
แนวคิดพื้นฐาน
มูลค่าเงินตามเวลา หรือ time value of money มีอยู่ว่า มูลค่าเงินจะเปลี่ยนแปลงไปตามระยะเวลา เงิน 1 บาทที่ได้มาในวันนี้ย่อมมีมูลค่ามากกว่าเงิน 1 บาทในอนาคต เพราะเงิน 1 บาทที่ได้มาแล้วสามารถนำไปลงทุนสร้างผลตอบแทนได้ตั้งแต่วันนี้ ในขณะที่เงินอนาคตจะสูญเสียโอกาสดังกล่าว นอกจากนี้ มูลค่าที่แท้จริงของเงินยังอาจถูกกัดกร่อนไปตามอัตราเงินเฟ้อ ทำให้มูลค่าที่แท้จริงของเงินจำนวนเท่ากันในอนาคตไม่เท่ากับมูลค่าแท้จริงของเงินในปัจจุบัน
โดยทั่วไป ผลตอบแทนของการฝากเงินหรือลงทุนจะอยู่ในรูปของอัตราดอกเบี้ย ปัจจัยที่กำหนดมูลค่าของเงินจึงได้แก่ ระยะเวลาและอัตราดอกเบี้ย
ตัวอย่าง 1 มูลค่าเงินตามเวลาของเงิน 100 บาท ที่นำไปฝากธนาคารที่อัตราดอกเบี้ย 2% เป็นระยะเวลา 3 ปี
เงิน 100 บาท ปีที่ 1 ดอกเบี้ย 2% ได้ดอกเบี้ย 2 บาท
เงิน 100 บาท ปีที่ 2 ดอกเบี้ย 2% ได้ดอกเบี้ย 2 บาท
เงิน 100 บาท ปีที่ 3 ดอกเบี้ย 2% ได้ดอกเบี้ย 2 บาทดังนั้น ภายหลังเวลา 3 ปี รวมได้ดอกเบี้ย 2 X 3 = 6 บาท เงินที่นำไปฝาก 100 บาทจงมีมูลค่าเพิ่มขึ้นเป็น 106 บาท จะเห็นว่าเมื่อเวลาผ่านไปมูลค่าเงินก็สูงขึ้นตามระยะเวลาในการลงทุน อย่างไรก็ตาม มูลค่าเงินที่เพิ่มขึ้นนี้เป็นการคำนวณดอกเบี้ยแบบง่ายเท่านั้น ในทางปฏิบัติ มูลค่าเงินที่เพิ่มขึ้นจริงต้องคำนวณแบบดอกเบี้ยทบต้น
ดอกเบี้ยแบบทบต้น (compound interest) คือ นำดอกเบี้ยที่ได้รับจากการฝากเงินแต่ละงวดมารวมเป็นเงินต้นของงวดต่อๆ ไป ซึ่งผลของดอกเบี้ยทบต้นนี้จะทำให้ดอกเบี้ยที่ได้รับในงวดต่อๆ ไปเพิ่มขึ้นเรื่อยๆ มูลค่าของเงินที่เพิ่มตามเวลายิ่งโตมากขึ้น เพราะได้ดอกเบี้ยบนดอกเบี้ยอีกชั้นหนึ่ง
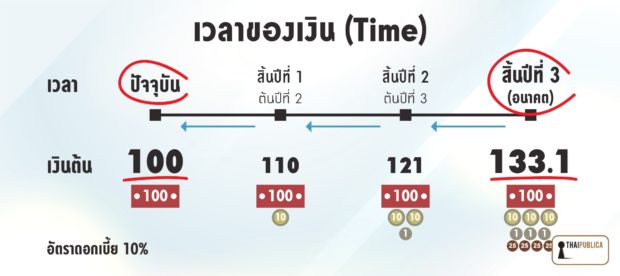
ตัวอย่าง 2 มูลค่าเงินตามเวลาของเงิน 100 บาท ที่นำไปฝากธนาคารที่อัตราดอกเบี้ยทบต้น 10 % เป็นระยะเวลา 3 ปี
สิ้นปีที่ 1 เงินต้น 100 บาท ดอกเบี้ย 10% ได้ดอกเบี้ย 10 บาท มูลค่าเงินเพิ่มเป็น 110 บาท
สิ้นปีที่ 2 เงินต้น 110 (100+10) บาท ดอกเบี้ย 10% ได้ดอกเบี้ย 11 บาท มูลค่าเงินเพิ่มเป็น 121 บาท
สิ้นปีที่ 3 เงินต้น 121 (110+10) บาท ดอกเบี้ย 10% ได้ดอกเบี้ย 12.1 บาท มูลค่าเงินเพิ่มเป็น 133.10 บาท
ภาพแสดงให้เห็นถึงมูลค่าเงินตามเวลาของเงินที่เป็นผลจากดอกเบี้ยทบต้นได้ชัดเจนขึ้น
จะเห็นได้ว่า สิ้นปีที่ 1 ได้ดอกเบี้ย 10 บาทนำไปรวมกับเงินต้น 100 บาท เป็น 110 บาท เงินต้นของการฝากเงินปีที่ 2 ซึ่งก็ได้ดอกเบี้ยมาอีก 11 บาท เมื่อนำมารวมกับเงินต้น 110 บาท ก็จะได้เงินต้นของปีที่ 3 เป็น 121 บาท รวมการฝากเงินทั้ง 3 ปี มูลค่าเงินเพิ่มเป็น 133.10 บาท จากผลของดอกเบี้ยทบต้น
มูลค่าอนาคต (Future Value)
เมื่อเข้าใจถึงผลกระทบของดอกเบี้ยและดอกเบี้ยทบต้นแล้ว สิ่งที่เราเริ่มจะบอกได้ก็คือมูลค่าของเงินในอนาคตของเงินก้อนหนึ่งๆ ภายใต้ช่วงเวลาและอัตราผลตอบแทนที่กำหนด เช่น จากตัวอย่างที่ 1 เมื่อนำเงิน 100 บาทไปฝากธนาคารที่อัตราดอกเบี้ย 2% ต่อปี เมื่อสิ้นปีที่ 1 ได้ดอกเบี้ยเพิ่มมา 2 บาท รวมมีเงิน 102 บาท เงิน 102 บาทนี้เองคือมูลค่าอนาคตของเงิน 100 บาท ณ สิ้นปีที่ 1 หรือในตัวอย่างที่ 2 เมื่อฝากครบ 3 ปี เงิน 133.1 บาท คือมูลค่าในอนาคตของเงินตั้งต้น 100 บาท ณ สิ้นปีที่ 3
มูลค่าปัจจุบัน
เมื่อเข้าใจหลักการหามูลค่าอนาคตแล้ว สิ่งที่เราจะเข้าใจตามมาก็คือมูลค่าปัจจุบัน กล่าวคือ เมื่อเรารู้อัตราดอกเบี้ยที่เกี่ยวข้องแล้ว เรามีเงิน 1 บาทในวันนี้ เราก็บอกได้ว่าในอนาคต เงิน 1 บาทนั้นจะมีมูลค่าเป็นเท่าไหร่ (เรียกว่า มูลค่าอนาคต) ในทางตรงกันข้าม หากเรารู้มูลค่าเงินในอนาคตที่ต้องการ เราก็คำนวณกลับมาได้ว่าต้องใช้ “มูลค่าปัจจุบัน” หรือเงินตั้งต้นเท่าไหร่ในการลงทุนหรือฝากธนาคารเพื่อให้ได้ดอกเบี้ยตามระยะเวลาจนมีเงินเท่ากับมูลค่าอนาคตตามเป้าหมาย โดยอัตราดอกเบี้ยที่ใช้คำนวณเงินในอนาคตกลับมาเป็นมูลค่าปัจจุบันนี้ เราเรียกว่า “อัตราคิดลด”
ตัวอย่าง 3 หากในระยะเวลา 3 ปี เราต้องการมีเงินในอนาคต 133.1 บาท โดยดอกเบี้ยอยู่ที่ 10% ต่อปี เราจะคำนวณเงินตั้งต้นที่เราจำเป็นต้องฝากธนาคาร/ลงทุนหรือมูลค่าปัจจุบันได้ตามนี้
สิ้นปีที่ 3 มูลค่าเงินอนาคต 133.10 บาท ดอกเบี้ย 10% ได้ดอกเบี้ย 12.1 บาทจากเงินต้น 121 บาท
สิ้นปีที่ 2 มูลค่าเงินอนาคต 121 บาทดอกเบี้ย 10% ได้ดอกเบี้ย 11 บาท จากเงินต้น 110 บาท
สิ้นปีที่ 1 มูลค่าเงินอนาคต 110 บาทดอกเบี้ย 10% ได้ดอกเบี้ย 10 บาท จากเงินต้น 100 บาท
ภาพแสดงมูลค่าปัจจุบันที่คำนวณจากมูลค่าในอนาคตด้วยอัตราคิดลด
จะเห็นได้ว่า เพื่อให้ได้เงิน 133.10 บาท จะต้องฝากเงินต้นจำนวน 100 บาทในปีที่ 1
เงินเฟ้อลิดรอนมูลค่า
อย่างไรก็ตาม เมื่อเวลาผ่านไปมูลค่าเงินมิใช่แต่จะเพิ่มขึ้นตามอัตราดอกเบี้ยอย่างเดียว เพราะหากเราไม่ได้เอาเงินไปฝากหรือไปลงทุนสร้างผลตอบแทน เงินเฟ้อย่อมทำให้อำนาจซื้อของเงิน 1 บาทลดลงทุกปี จนมูลค่าอนาคตอาจน้อยลงกว่ามูลค่าของเงินในปัจจุบันได้ เพราะของแพงขึ้น กล่าวอีกนัยหนึ่ง สินค้าที่วันหนึ่งเคยมีราคา 100 บาท เมื่อระยะเวลาผ่านไปราคาย่อมปรับขึ้นตามอัตราเงินเฟ้อ ทำให้เงิน 100 บาท ไม่สามารถซื้อสินค้านั้นได้อีกต่อไป
ตัวอย่าง 4 มูลค่าเงินตามเวลาของเงิน 100 บาท ที่เปลี่ยนแปลงไปจากการเสียโอกาสลงทุนในระยะเวลา 3 ปี และผลจากเงินเฟ้อ ณ อัตราเงินเฟ้อ 2%
เงิน 100 บาท ปีที่ 1 เงินเฟ้อ 2% สิ้นปีเงินหายไป 2 บาท มูลค่าเงินที่แท้จริงลดลงเหลือ 98 บาท
เงิน 98 บาท ปีที่ 2 เงินเฟ้อ 2% สิ้นปีเงินหายไป 2 บาท มูลค่าเงินที่แท้จริงลดลงเหลือ 96.04 บาท
เงิน 96.04 บาท ปีที่ 3 เงินเฟ้อ 2% สิ้นปีเงินหายไป 2 บาท มูลค่าเงินที่แท้จริงลดลงเหลือ 94.12 บาท
แสดงให้เห็นว่าอำนาจซื้อของเงิน 100 บาทในอีก 3 ปีข้างหน้าเหลือเพียง 94.12 บาท หรือกล่าวอีกนัยหนึ่ง หากไม่ได้ลงทุน เงินจำนวน 94.12 บาท จะเป็นมูลค่าอนาคตของเงิน 100 บาทในวันนี้ แต่หากเรานำเงินไปลงทุนที่ให้ผลตอบแทนที่สูงกว่าเงินเฟ้อ มูลค่าอนาคตก็จะเพิ่มขึ้นมากกว่าจำนวนเงินในปัจจุบัน
ตัวอย่าง 5 ในสถานการณ์ที่เรามีเงิน 100 บาท สินค้ามีราคา 100 บาท อัตราเงินเฟ้อ 2% ต่อปี อัตราดอกเบี้ย 5% ต่อปี มูลค่าตามเวลาของเงินจะทำให้เราเห็นภาพทางเลือกทางการเงินเป็นดังต่อไปนี้
ทางเลือกแรก ใช้เงินวันนี้ 100 บาทไปซื้อสินค้าราคา 100 บาททันที เพราะหากช้า เงินเฟ้อจะทำให้สินค้าเดิมมีราคาเพิ่มเป็น 102 บาท และทำให้เงิน 100 บาท ไม่พอซื้ออีกต่อไป
ทางเลือกที่สอง ยังไม่ซื้อสินค้าแต่นำเงินไปฝากธนาคารได้ดอกเบี้ย 5% ต่อปี ฝากครบ 1 ปี ได้ดอกเบี้ย 5 บาท มีเงินเพิ่มเป็น105 บาท แล้วนำไปซื้อสินค้าที่มีราคาเพิ่มเป็น 102 บาท และยังมีเงินเหลืออีก 3 บาท
โดยกล่าวได้ว่าในเงิน 5 บาท ที่เพิ่มขึ้นมา 2 บาท ถือเป็นผลตอบแทนที่ชดเชยเงินเฟ้อ ส่วนอีก 3 บาท จะถือเป็น “ผลตอบแทนที่แท้จริง”
มูลค่าเงินตามเวลาช่วยในการตัดสินใจ
เมื่อรู้ว่ามูลค่าเงินในปัจจุบันมีค่ามากกว่าเงินในอนาคต เพราะเงินในวันนี้สามารถนำไปลงทุนและสร้างผลตอบแทน ก็จะช่วยให้ตัดสินใจทุกอย่างที่เกี่ยวกับเงินได้ดีขึ้น ไม่ว่าจะเลือกใช้เงินวันนี้หรือเลือกใช้วันหน้า หรือจะเลือกลงทุนเพื่อให้เงินโตขึ้น
โดยทั่วไป กิจการต่างๆ มีการลงทุนอย่างกว้างขวางในหลายประเภท การตัดสินใจของผู้บริหารนอกจากพิจารณาความเสี่ยงอย่างรอบคอบแล้ว ควรคำนึงถึงผลตอบแทนบนแนวคิดมูลค่าเงินตามเวลาด้วย มีหลายกิจการที่ใช้เฉพาะระยะเวลาคืนทุนมาประกอบการตัดสินใจ ด้วยการประเมินกระแสเงินคืนหรือมูลค่าปัจจุบันเท่ากันทุกปี ซึ่งทำให้ผลตอบแทนที่จริงต่ำกว่าที่ควรจะเป็น เช่น หากเราลงทุนไป 100 บาท และประเมินว่าหากได้เงินคืนกลับมาปีละ 10 บาท 10 ปี ก็จะคุ้มทุน ถือว่าไม่ถูกต้อง เพราะเงินจำนวนเท่ากันแต่ละปีจะมีมูลค่าไม่เท่ากัน ยิ่งนานไป เงินจำนวนเท่ากันจะมีมูลค่าน้อยลง ดังนั้น แม้จะครบ 10 ปี ก็ยังไม่อาจเรียกได้ว่าคุ้มทุน
นอกจากนั้น ความรู้เรื่องมูลค่าเงินตามเวลาอาจทำให้เราตัดสินใจใช้เงินในวันนี้ไปกับการลงทุน การกู้เงินเพื่อเพิ่มผลตอบแทนให้มากขึ้นได้ ตัวอย่างเช่น ก เป็นนักลงทุน มีเงินและมีทางเลือกในการลงทุนที่ผลตอบแทนค่อนข้างแน่นอน โดยผลตอบแทนของการลงทุนอยู่ที่ 5% ซึ่ง หาก ก มีเงิน 100 บาท ต้องการผลตอบแทนที่ 5% ก็ลงทุนได้เลย นับว่าเป็นผลตอบแทนที่น่าพอใจ แต่นอกจากนี้ ก ยังมีทางเลือกที่จะทำให้ผลตอบแทนมากขึ้นไปอีก ด้วยการกู้เงินมาลงทุน
โดยจากที่มีเงิน 100 บาท กู้เพิ่ม 50 บาท อัตราผลตอบแทนการลงทุนอยู่ที่ 10% แต่ต้องจ่ายดอกเบี้ย 5% ดังนั้น ก มีเงินรวม 150 บาท ที่จะไปลงทุน การลงทุนของ ก ในกรณีนี้มีโอกาสทั้งที่จะได้ผลตอบแทนที่สูงขึ้น แต่ก็มีโอกาสที่จะขาดทุนมากขึ้นเช่นกันจากความเสี่ยงที่เพิ่มขึ้น ตามตัวอย่างดังต่อไปนี้
กรณีได้ผลตอบแทน มีเงินส่วนตัว 100 บาท กู้เงิน 50 บาท ได้ผลตอบแทน 10%
เงินส่วนตัว 100 บาท ผลตอบแทน 10% ได้เงิน 10 บาท รวมเป็นเงิน 110
เงินกู้ 50 บาท ผลตอบแทน 10% ได้เงิน 5 บาท รวมเป็นเงิน 55 บาท
รวมทั้งหมดมีเงิน 165 บาท
จ่ายคืนเงินกู้ 50 บาท ที่กู้มาในอัตราดอกเบี้ย 5% คิดดอกเบี้ยได้ 2.5 บาท รวมต้องจ่ายคืน 52.5 บาท
ใช้เงินที่ได้มา 55 บาท จ่ายหนี้ 52.5 บาท ยังเหลือเงิน 2.5 บาท
เมื่อรวมกับเงินส่วนตัวที่เพิ่มเป็น 110 บาท จะมีเงินรวม 112.5 บาท
กรณีขาดทุน มีเงินส่วนตัว 100 บาท กู้เงิน 50 บาท ขาดทุน 10%
เงินส่วนตัว 100 บาท ขาดทุน 10% คิดเป็นเงิน 10 บาท เหลือเงิน 90
เงินกู้ 50 บาท ขาดทุน 10% คิดเป็นเงิน 5 บาท เหลือเงิน 45
รวมเงินเหลือ 135 บาท
จ่ายคืนเงินกู้ 50 บาท ที่กู้มาในอัตราดอกเบี้ย 5% คิดดอกเบี้ยได้ 2.5 บาท รวมต้องจ่ายคืน 52.5 บาท
ดังนั้นเงินจะเหลือ 135-52.5 = 82.5 บาท
จะเห็นได้ว่า การกู้เงินหรือสร้างหนี้มาลงทุนมีความเสี่ยงในตัวเอง ไม่ว่าจะเป็นการกู้เงินมาทำโครงการ หรือ การซื้อหุ้นบัญชีมาร์จิน (margin account) ที่ใช้เงินตัวเองส่วนหนึ่ง กู้เพื่อลงทุนอีกส่วนหนึ่ง เจ้าของเงินต้องประเมินให้ดี หากมั่นใจและประเมินว่ามีความเสี่ยงต่ำ การกู้เงินจะช่วยเพิ่มผลตอบแทนได้ แต่ก็มีโอกาสที่ผลตอบแทนจะไม่เป็นไปตามคาด และทำให้ขาดทุนมากกว่าปกติได้
แต่ไม่ว่าจะอย่างไรก็ตาม เมื่อเข้าใจแล้วว่ามูลค่าเงินมีการเปลี่ยนแปลงไปตามระยะเวลา โดยหากปล่อยทิ้งไว้เฉยๆ อำนาจซื้อของเงินจะลดลงจากเงินเฟ้อ แต่หากนำไปลงทุน มูลค่าอนาคตของเงินนั้นก็จะมักสูงกว่าจำนวนเงินตั้งต้นในปัจจุบัน ย่อมอาจกล่าวได้ว่า ควรตัดสินใจเรื่องการลงทุนตั้งแต่วันนี้ เพราะ “เวลาเป็นเงินเป็นทอง”
ซีรีย์ Financial literacy สนับสนุนโดยกลุ่มธุรกิจการเงินเกียรตินาคินภัทร