สฤณี อาชวานันทกุล
ผู้เขียนเขียนเรื่อง “อินโฟกราฟฟิกที่ดี” ติดต่อกันมาแล้วสามตอน ตอนสุดท้ายในซีรีส์นี้ตั้งใจจะพูดถึงกับดักทางสถิติที่พบเห็นบ่อยแต่ไม่ค่อยมีใครฉุกคิดว่าติดกับดัก รวมทั้งตัวคนที่ออกแบบอินโฟกราฟฟิกเองด้วย โชคดีที่ไปเจอเว็บ School of Data ซึ่งมีชุดบทความอ่านง่ายเกี่ยวกับการทำความเข้าใจและจัดการกับข้อมูล รวมถึงบทความเกี่ยวกับความเข้าใจผิดเกี่ยวกับสถิติ ผู้เขียนจึงถือวิสาสะแปลเป็นภาษาไทยเพื่อเผยแพร่โดยทั่วกัน
ระวัง! ความเข้าใจผิดพบบ่อยและวิธีหลีกเลี่ยง
แปลจาก Look Out! Common Misconceptions and How to Avoid Them, เว็บไซต์ School of Data
คุณเคยได้ยินคำกล่าวยอดฮิต “การโกหกมีอยู่สามแบบ – คำโกหก โคตรโกหก และสถิติ” หรือเปล่า? ประโยคนี้สะท้อนความไม่ไว้วางใจของคนทั่วไปต่อข้อมูลที่เป็นตัวเลขและวิธีแสดงข้อมูล ซึ่งความไม่ไว้ใจนี้ก็มีมูลความจริงไม่น้อย เพราะนานเกินไปแล้วที่การแสดงข้อมูลตัวเลขในรูปกราฟถูกใช้บิดเบือน “ข้อเท็จจริง” ให้คนเข้าใจผิด คำอธิบายต่อเรื่องนี้คือ ข้อมูลทั้งหมดล้วนอยู่ในข้อมูลดิบ แต่ก่อนที่เราจะประมวลผลข้อมูลดิบ มันก็ ‘เยอะ’ เกินกว่าที่สมองของเราจะเข้าใจได้
การคำนวณหรือการแสดงข้อมูลเป็นภาพ (visualization) ใดๆ ก็ตาม ไม่ว่าจะง่ายดายอย่างการคำนวณค่าเฉลี่ย หรือซับซ้อนอย่างการแสดงกราฟสามมิติ ล้วนตั้งอยู่บนการยอม “สูญเสีย” ข้อมูลบางส่วนไป เพื่อให้เราทำความเข้าใจกับมันได้ ความผิดพลาดส่วนใหญ่เกิดขึ้นเวลาที่คนทิ้งข้อมูลส่วนที่สำคัญจริงๆ ไป หรือไม่ก็พยายามอธิบายข้อมูลทั้งชุดด้วยประโยคใหญ่ๆ ที่ฟังดูครอบจักรวาล โดยมากสิ่งที่พวกเขาบอกเรามักจะ “จริง แต่ไม่ได้บอกเรื่องราวทั้งหมด”
วันนี้เราจะมาดูความเข้าใจผิดและกับดักทางความคิดที่พบบ่อยเวลาที่คนเริ่มวิเคราะห์ข้อมูลเพื่อแสดงด้วยภาพ คุณจะหลีกเลี่ยงความผิดพลาดในงานของคุณ และไม่ตกหลุมพรางในงานของคนอื่น ก็ต่อเมื่อคุณรู้ว่าความผิดพลาดเหล่านั้นมีอะไรบ้าง
กับดักค่าเฉลี่ย
คุณเคยเจอประโยคอย่าง “ชาวยุโรปเฉลี่ยดื่มเบียร์ 1 ลิตรต่อวัน” หรือเปล่า? คุณถามตัวเองไหมว่า “ชาวยุโรปเฉลี่ย” ผู้ลึกลับคนนี้เป็นใคร และคุณจะเจอเขาได้ที่ไหน? ข่าวร้ายคือไม่มีวันเจอ เพราะเขาหรือเธอไม่มีอยู่จริง ในบางประเทศคนดื่มไวน์มากกว่าเบียร์ แล้วคนที่ไม่ดื่มเหล้าเลยล่ะ? เด็กๆ ล่ะ? พวกเขาดื่มเบียร์วันละ 1 ลิตรด้วยหรือเปล่า? ชัดเจนว่าประโยคนี้ชี้ชวนให้เข้าใจผิด แล้วตัวเลขนี้มาจากไหนกัน?
คนที่อ้างอะไรๆ ทำนองนี้มักจะตั้งต้นจากตัวเลขใหญ่ๆ บางตัว เช่น ทุกปีชาวยุโรปทั้งทวีปดื่มเบียร์รวมกัน 109,000 ล้านลิตร เสร็จแล้วพวกเขาก็เอาตัวเลขนี้มาหารด้วยจำนวนวันในหนึ่งปีและจำนวนประชากรของยุโรป เสร็จแล้วก็ป่าวร้องข่าวน่าตื่นเต้น ถ้าเราเอางบประมาณด้านสาธารณสุขมาหารด้วยประชากร ผลที่ได้ก็ออกมาทำนองเดียวกัน มันแปลว่าคนทุกคนใช้เงินเท่านี้หรือเปล่า? เปล่าเลย มันแปลว่าบางคนใช้มากกว่า บางคนใช้น้อยกว่า สิ่งที่เราทำคือการหา ค่าเฉลี่ย ซึ่งบอกอะไรๆ ได้ดีมาก – ถ้าหากข้อมูลกระจายตัวแบบปกติ “การกระจายตัวแบบปกติ” (normal distribution) หมายถึงเส้นโค้งความถี่รูประฆังคว่ำ
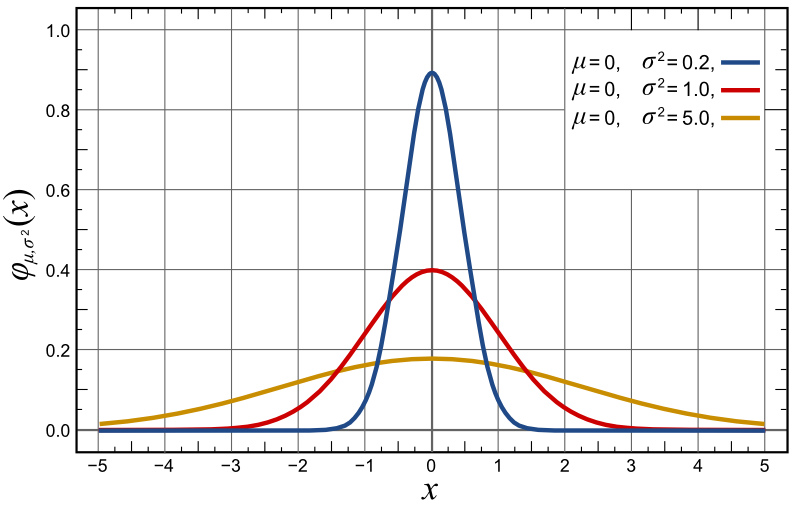
ภาพด้านบนแสดงการกระจายตัวแบบปกติสามชุด (แสดงด้วยเส้นสามเส้น) ทุกชุดมี ค่าเฉลี่ย เท่ากัน แต่ก็ชัดเจนว่ามันไม่เหมือนกัน สิ่งที่ค่าเฉลี่ยบอกคุณไม่ได้คือขอบเขตของข้อมูล
ข้อมูลส่วนใหญ่ที่เราเจอไม่ได้กระจายตัวแบบปกติ ตัวอย่างหนึ่งคือรายได้ ตัวเลขรายได้เฉลี่ย (สิ่งที่สื่อมักจะชอบรายงาน) จะทำให้คิดว่าคนครึ่งหนึ่งมีรายได้มากกว่าค่านี้ อีกครึ่งหนึ่งน้อยกว่าค่านี้ แต่ความคิดนี้ผิด ในประเทศส่วนใหญ่ คนที่มีรายได้น้อยกว่าค่าเฉลี่ยมีจำนวนมากกว่าคนที่มีรายได้สูงกว่าค่าเฉลี่ยหลายเท่า ยังไงล่ะ? ก็เพราะว่ารายได้ไม่ได้กระจายตัวแบบปกติ มันพุ่งถึงจุดสูงสุด ณ จุดหนึ่ง (คือครัวเรือนจำนวนมากที่สุดมีรายได้ระดับนี้) แล้วทิ้งหางยาวไปทางรายได้สูงๆ
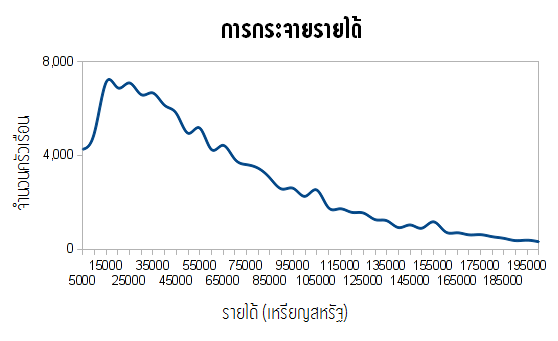
กราฟด้านบนแสดงการกระจายตัวของรายได้ในสหรัฐอเมริกา จากสำมะโนประชากรปี 2011 สำหรับครัวเรือนที่มีรายได้แต่ละระดับ สูงสุดที่ 200,000 เหรียญสหรัฐ คุณจะเห็นว่าครัวเรือนส่วนใหญ่มีรายได้ระหว่าง 15,000-65,000 เหรียญสหรัฐ แต่เรามีหางยาวซึ่งดึงค่าเฉลี่ยให้เบ้ขึ้น
ถ้าหากรายได้เฉลี่ยปรับตัวสูงขึ้น มันก็อาจเป็นเพราะคนส่วนใหญ่มีรายได้เพิ่มขึ้น แต่มันก็อาจเกิดจากการที่คนในกลุ่มรายได้สูงสุดมีรายได้เพิ่มมหาศาลเช่นกัน – ทั้งสองกรณีนี้จะดันค่าเฉลี่ยขึ้น
ทดสอบ: ถ้าคุณอยากลองคิดเรื่องนี้กับตัวเลข ลองทำบททดสอบสั้นๆ นี้ดู:
นึกถึงคน 10 คน คนแรกได้เงินเดือน 1 บาท คนที่สองได้ 2 บาท คนที่สามได้ 3 บาท …ไปเรื่อยๆ ถึงคนสุดท้ายได้ 10 บาท ลองคำนวณเงินเดือนเฉลี่ยดู
ทีนี้เพิ่มเงินให้ทุกคนคนละ 1 บาท (เป็น 2 บาท, 3 บาท, 4 บาท… ถึง 11 บาท) ค่าเฉลี่ยใหม่เท่ากับเท่าไหร่?
คราวนี้กลับไปที่เงินเดือนตั้งต้น (1 บาท, 2 บาท, 3 บาท ฯลฯ) แล้วบวก 10 บาทให้กับคนที่ได้เงินเดือนสูงสุด (จะได้ 1 บาท, 2 บาท, 3 บาท, …. 9 บาท และ 20 บาท) คราวนี้ค่าเฉลี่ยเท่ากับเท่าไหร่?
นักเศรษฐศาสตร์ตระหนักในประเด็นนี้ พวกเขาเลยเพิ่มตัววัดเข้ามา “ค่าสัมประสิทธิ์จีนี่” (Gini coefficient) บอกคุณเกี่ยวกับการกระจายตัวของรายได้ วิธีคำนวณค่านี้ซับซ้อนเล็กน้อยและอยู่นอกเหนือบทความชิ้นนี้ อย่างไรก็ดี คุณก็ควรรู้ว่ามีตัววัดแบบนี้อยู่ เราสูญเสียข้อมูลมหาศาลไปเวลาที่คำนวณแต่ค่าเฉลี่ย นึกถึงเรื่องนี้ให้มากเวลาที่คุณอ่านข่าวและเนื้อหาออนไลน์
ทดสอบ: คุณมองเห็นตัวอย่างอื่นอีกไหมที่การใช้ค่าเฉลี่ยมีปัญหา?
มากกว่าแค่ค่าเฉลี่ย…
แล้วถ้าเราไม่ใช้ ค่าเฉลี่ย เราควรใช้อะไรดี? มีตัววัดอื่นๆ อีกมากมายที่สามารถสร้างบริบทเพิ่มเติมให้ตัวเลขค่าเฉลี่ยมีความหมายมากกว่าเดิมได้ ยกตัวอย่างเช่น
- แสดงค่าเฉลี่ยพร้อมกับขอบเขตข้อมูลด้วย เช่น บอกว่าข้อมูลชุดนี้มีค่า 20-5,000 และมีค่าเฉลี่ยเท่ากับ 50 ลองนึกถึงตัวอย่างเบียร์ของเราก็ได้ – จะดีกว่าเดิมเล็กน้อยถ้าคุณบอกว่าชาวยุโรปดื่มเบียร์ระหว่าง 0-5 ลิตรต่อวัน เฉลี่ยคนละ 1 ลิตรต่อวัน
- ใช้ ค่ามัธยฐาน: ค่ามัธยฐานคือมูลค่าที่อยู่ตรงกลางพอดี คือมี 50% ที่อยู่สูงกว่าและอีก 50% อยู่ต่ำกว่า รายได้มัธยฐานหมายถึงรายได้ที่คนจำนวน 50% มีรายได้น้อยกว่าค่านี้ คนที่เหลืออีก 50% มีรายได้สูงกว่าค่านี้
- ใช้ ค่าควอไทล์ หรือ เปอร์เซ็นต์ไทล์: ควอไทล์ (quartile) เหมือนกับค่ามัธยฐานแต่ใช้สำหรับระดับ 25 เปอร์เซ็นต์, 50 เปอร์เซ็นต์ และ 75 เปอร์เซ็นต์ เปอร์เซ็นต์ไทล์ (percentile) ก็เหมือนกันแต่ใช้สำหรับช่วงอื่นที่ไม่ใช่ทุกๆ เศษหนึ่งส่วนสี่ (ปกติทีละ 10 เปอร์เซ็นต์) ค่าเหล่านี้ให้ข้อมูลเรามากกว่าค่าเฉลี่ยมาก นอกจากนั้นยังบอกเราเกี่ยวกับการกระจายตัวของข้อมูลด้วย (เช่น คน 1 เปอร์เซ็นต์ที่รวยที่สุดครอบครองความมั่งคั่ง 80 เปอร์เซ็นต์ของทั้งประเทศจริงๆ หรือเปล่า?)
ขนาดนั้นสำคัญไฉน
ขนาดนั้นสำคัญจริงๆ ในการแสดงข้อมูลด้วยภาพ ลองเปรียบเทียบกราฟแท่งสองกราฟต่อไปนี้
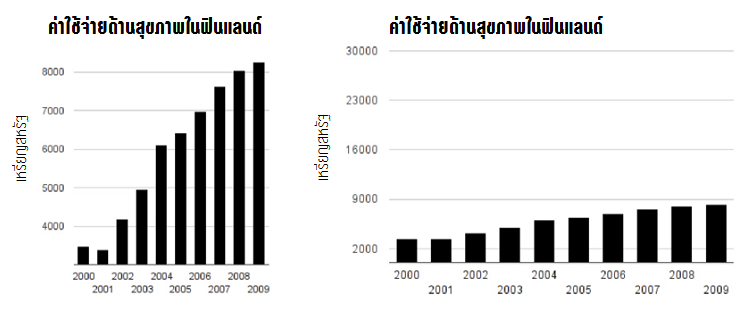
ลองนึกถึงพาดหัวของกราฟสองกราฟนี้ พาดหัวสำหรับกราฟทางซ้ายอาจเขียนว่า “ค่าใช้จ่ายด้านสุขภาพในฟินแลนด์พุ่งฉุดไม่อยู่!” ส่วนกราฟทางด้านขวาอาจอยู่ใต้พาดหัว “ค่าใช้จ่ายด้านสุขภาพในฟินแลนด์ค่อนข้างทรงตัว” ทีนี้ลองดูข้อมูล มันคือข้อมูลชุดเดียวกันแต่นำเสนอเป็นสองวิธี (ที่ไม่ถูกทั้งคู่)
ทดสอบ: คุณมองเห็นไหมว่ากราฟข้างต้นทำให้คนเข้าใจผิดอย่างไร?
ก่อนอื่น ข้อมูลในกราฟทางด้านซ้ายไม่ได้เริ่มที่ 0 เหรียญสหรัฐ แต่เริ่มที่ประมาณ 3,000 เหรียญสหรัฐ ทำให้ความแตกต่างระหว่างแท่งดูใหญ่กว่าความเป็นจริง เช่น ค่าใช้จ่ายระหว่างปี 2001 กับ 2002 ดูเหมือนจะเพิ่มขึ้นอย่างน้อยสามเท่า! ทั้งที่ความจริงไม่ใช่เลย นอกจากนี้ การเลือกแกนตั้งและแกนนอนให้มีความยาวเท่ากัน (ทำให้กราฟอยู่ในกรอบสี่เหลี่ยมจัตุรัส) ก็ช่วยขับเน้นความแตกต่างให้ดูหวือหวาเข้าไปอีก
กราฟทางด้านขวาเริ่มต้นที่ 0 เหรียญสหรัฐ แต่ลากหน่วยในแกนตั้งขึ้นไปถึง 30,000 เหรียญสหรัฐ ทั้งที่ค่าสูงสุดในชุดข้อมูลอยู่ที่ 9,000 เหรียญสหรัฐเท่านั้น กราฟนี้ เที่ยงตรงกว่า กราฟทางซ้ายมือ แต่ก็ยังทำให้สับสนอยู่ดี ไม่น่าแปลกใจว่าทำไมคนที่คุ้นเคยกับการหลอกลวงคนอื่นด้วยข้อมูลถึงได้คิดว่าสถิติคือเรื่องโกหก
ตัวอย่างนี้ชี้ให้เห็นว่าการแสดงข้อมูลของคุณด้วยภาพนั้นสำคัญเพียงใดที่จะต้องถูกต้อง ต่อไปนี้เป็นกฎง่ายๆ บางข้อ –
- เลือกขอบเขตที่เหมาะสมกับข้อมูลของคุณเสมอ
- ระบุขอบเขตอย่างถูกต้องบนแกน!
- ความเปลี่ยนแปลงของขนาดที่เรามองเห็นในกราฟควรสะท้อนความเปลี่ยนแปลงของขนาดในข้อมูลของคุณ ฉะนั้นถ้าหากข้อมูลของคุณแสดงว่า B มีค่าเท่ากับสองเท่าของ A ขนาดของ B ก็ควรใหญ่เป็นสองเท่าของ A ในภาพ
กฎ “แสดงขนาดให้ถูกต้อง” นั้นยากกว่าเดิมเวลาวาดภาพสองมิติ (คือไม่ใช่กราฟเส้น ซึ่งมีหนึ่งมิติ) เมื่อคุณต้องคำนึงถึงพื้นที่รวม เมื่อไหร่ก็ไม่รู้ที่สำนักข่าวต่างๆ เริ่มเลิกใช้กราฟแท่ง เปลี่ยนมาใช้ภาพสองมิติแต่ยังขยายขนาด (scale) ของภาพด้วยวิธีเดิม ปัญหาน่ะหรือ? ถ้าคุณปรับความสูงของรูปให้สะท้อนความเปลี่ยนแปลงและความกว้างของมันก็ขยายขึ้นด้วยโดยอัตโนมัติ พื้นที่ก็จะขยายเพิ่มยิ่งกว่าเดิมและทำให้ข้อมูลผิดถนัด! งงไหม? ลองดูฟองสบู่ด้านล่างนี้
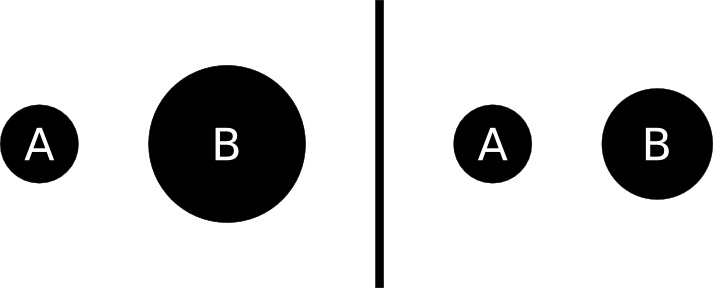
ทดสอบ: เราอยากแสดงว่า B มีขนาดเป็นสองเท่าของ A ภาพไหนที่ถูกต้อง? เพราะอะไร?
คำตอบ: ภาพทางขวามือ
ลืมหรือยังว่าสูตรการคำนวณพื้นที่ของวงกลมคืออะไร? (พื้นที่ = πr² ถ้าหากคุณไม่คุ้นเลย ลองดูหน้านี้) ในภาพทางซ้าย รัศมีของวงกลม A ถูกขยายขึ้นสองเท่า นั่นหมายความว่าพื้นที่รวมใหญ่ขึ้นถึงสี่เท่า! นี่คือการแสดงข้อมูลที่ผิด ถ้าวงกลม B จะแสดงตัวเลขที่ใหญ่เป็นสองเท่าของ A เราก็ต้องคำนวณให้พื้นที่ B ใหญ่เป็นสองเท่าของพื้นที่ A ซึ่งแปลว่าเราต้องลดความยาวของรัศมีลง √2 เพื่อแสดงความแตกต่างของขนาดที่ถูกต้อง
เวลาจะบอกได้?
เส้นเวลามักจะขาดไม่ได้เวลาแสดงข้อมูล ลองดูกราฟต่อไปนี้
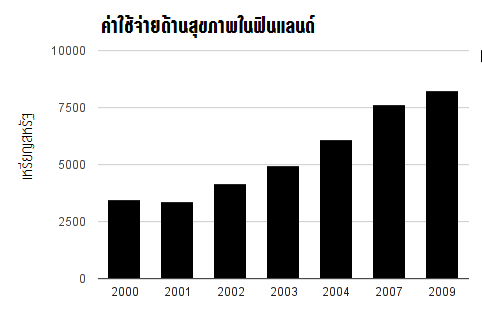
ดูเหมือนค่าใช้จ่ายด้านสุขภาพจะเพิ่มขึ้นอย่างคงที่ต่อเนื่องตั้งแต่ปี 2002 ใช่ไหม? ไม่เชิง ลองสังเกตว่าก่อนปี 2004 แกนนอนแสดงข้อมูลทีละ 1 ปี แต่หลังจากนั้นมีช่องว่างระหว่างปี 2004 กับ 2007 และจาก 2007 ก็กระโดดไป 2009 การแสดงข้อมูลแบบนี้ทำให้เราเชื่อว่าค่าใช้จ่ายด้านสุขภาพเพิ่มขึ้นอย่างต่อเนื่องในอัตราการเติบโตคงที่ตั้งแต่ปี 2002 ทั้งที่ความจริงไม่ใช่ ฉะนั้นถ้าคุณแสดงเส้นเวลา คุณก็ควรจะมั่นใจว่าช่องห่างระหว่างจุดข้อมูลต่างๆ นั้นถูกต้อง! ไม่อย่างนั้นคุณจะไม่มีวันมองเห็นแนวโน้มที่แท้จริงได้เลย
สหสัมพันธ์ไม่ใช่เหตุปัจจัย
ความเข้าใจผิดว่า “สหสัมพันธ์” (correlation หมายถึงชุดข้อมูลสองชุดที่เดินทางเดียวกัน หรือเดินสวนทางกัน) แสดงความสัมพันธ์แบบเป็นเหตุเป็นผลกันนั้นแพร่หลายเสียจนในวิกิพีเดียมีบทความอธิบายเรื่องนี้โดยเฉพาะ เราคงไม่มีอะไรจะเพิ่มเติมในที่นี้ สรุปสั้นๆ คือ ลำพังการที่ข้อมูลสองจุดแสดงการเปลี่ยนแปลงที่อาจมีความสัมพันธ์กัน ไม่ได้แปลว่าจุดหนึ่งก่อให้เกิดอีกจุดหนึ่ง (ยกตัวอย่างเช่น ถ้ากบร้องทุกครั้งที่ฝนตก แปลว่า “ฝนตก” อาจสัมพันธ์กับ “กบร้อง” แต่ลำพังข้อมูลนี้ไม่ได้แปลว่า “กบร้อง” ทำให้ “ฝนตก”)
บริบท, บริบท, บริบท
ประเด็นหนึ่งที่สำคัญยิ่งสำหรับข้อมูลคือบริบทของข้อมูล ตัวเลขหรือคุณภาพไม่มีความหมายใดๆ เลยถ้าหากคุณไม่อธิบายบริบท ดังนั้นคุณถึงต้องอธิบายว่ากำลังแสดงอะไรอยู่ อธิบายว่าคุณอ่านข้อมูลอย่างไร อธิบายว่าข้อมูลมาจากไหน และอธิบายว่าคุณทำอะไรกับมัน ถ้าคุณมอบบริบทที่เหมาะสม บทสรุปก็ควรจะ ‘กระโดด’ ออกมาจากข้อมูลนั้นเอง
เปอร์เซ็นต์ กับ จุด (percentage point) ที่เปลี่ยนแปลง
ข้อนี้เป็นกับดักสำหรับเราหลายคน ถ้าหากตัวเลขเปลี่ยนแปลงจาก 5 เปอร์เซ็นต์ เป็น 10 เปอร์เซ็นต์ การเปลี่ยนแปลงนี้คิดเป็นกี่เปอร์เซ็นต์?
ถ้าคุณตอบว่า 5 เปอร์เซ็นต์ เสียใจด้วยนะ! คำตอบคือ 100 เปอร์เซ็นต์ (10 เปอร์เซ็นต์ เท่ากับ 200 เปอร์เซ็นต์ ของ 5 เปอร์เซ็นต์) หรือเปลี่ยนไป 5 จุด ดังนั้นก็ระวังให้ดีในคราวต่อไปที่คุณเห็นคนรายงานผลการเลือกตั้ง ผลการสำรวจความคิดเห็นและอื่นๆ ทำนองนี้ คุณจะมองเห็นข้อผิดพลาดของพวกเขาหรือไม่?
อยากทบทวนวิธีคำนวณเปอร์เซ็นต์ที่เปลี่ยนแปลงหรือเปล่า? ลองดู หน้านี้ของเว็บ Math is Fun
จับขโมย – ความอ่อนไหวกับตัวเลขใหญ่ๆ
ลองนึกดูว่าคุณเป็นเจ้าของร้านค้า เพิ่งติดตั้งระบบสัญญาณกันขโมย ระบบนี้สามารถเตือนภัยด้วยอัตราความเที่ยงตรงถึง 99 เปอร์เซ็นต์ วันหนึ่งสัญญาณดังขึ้นมา มีความเป็นไปได้เท่าไรที่คนที่เดินผ่านระบบนี้จะเป็นขโมย?
คุณอาจจะอยากตอบว่ามีความเป็นไปได้ 99 เปอร์เซ็นต์ที่คนคนนั้นขโมยอะไรสักอย่างในร้าน แต่ความจริงอาจไม่เป็นอย่างนั้นก็ได้
ในร้านของคุณมีทั้งลูกค้าที่ซื่อสัตย์กับหัวขโมย แต่ลูกค้าที่ซื่อสัตย์มีจำนวนมากกว่าหัวขโมยมาก – มีลูกค้าที่ซื่อสัตย์ 10,000 คน และมีหัวขโมยเพียงคนเดียว ถ้าหากคนทุกคนเดินผ่านระบบเตือนภัยของคุณ สัญญาณจะดัง 101 ครั้ง 1 เปอร์เซ็นต์ของเวลาที่ดังมันจะชี้คนผิด คือดังเวลาลูกค้าดีเดินผ่าน ดังนั้นมันจะดังอย่างถูกต้อง 100 ครั้ง ระบบจะบอกอย่างถูกต้องว่าหัวขโมยคือหัวขโมย 99 เปอร์เซ็นต์ของเวลาดัง ฉะนั้นมันจึงน่าจะดังหนึ่งครั้งเวลาที่ขโมยตัวจริงเดินผ่าน แต่จากจำนวนครั้งทั้งหมด 101 ครั้งที่สัญญาณดัง จะมีเพียง 1 ครั้งเท่านั้นที่มีหัวขโมยอยู่ในร้านคุณจริงๆ ดังนั้นความเป็นไปได้ที่คนคนนั้นจะเป็น ขโมยตัวจริง เวลาสัญญาณดังจึงไม่ถึง 1 เปอร์เซ็นต์ (จริงๆ คือ 1 / 101 = 0.99 เปอร์เซ็นต์)
การประเมินความเป็นไปได้สูงเกินไปในกรณีที่เหตุการณ์อะไรสักอย่างถูกรายงานว่าเกิดจริงแบบนี้มีชื่อเรียกว่า “ตรรกะวิบัติเรื่องอัตราฐาน” (base rate fallacy) ซึ่งเป็นคำอธิบายว่าทำไมการค้นตัวที่สนามบินและวิธีคัดกรองคนอื่นๆ จึงทึกทักว่าผู้โดยสารจำนวนมากเป็นผู้ก่อการร้าย (false positive)
สรุป
ในส่วนนี้เราทบทวนความผิดพลาดที่พบบ่อยบางประการเวลานำเสนอข้อมูล ไม่ว่าจะใช้ข้อมูลเป็นเครื่องมือเล่าเรื่องราว หรือสื่อสารประเด็นและข้อค้นพบของเรา ถึงแม้เราจะต้อง “ย่อย” ข้อมูลให้เข้าใจง่ายว่าข้อมูลแปลว่าอะไร การย่อยอย่างผิดๆ ก็อาจทำให้คนเข้าใจผิด เมื่อใดก็ตามที่คุณใช้ภาพแสดงหลักฐาน พยายามซื่อสัตย์กับข้อมูลให้มากที่สุด ถ้าเป็นไปได้ก็อย่าเผยแพร่เฉพาะผลการวิเคราะห์ของคุณอย่างเดียว แต่จงปล่อยข้อมูลดิบออกมาพร้อมกันเลย!
—–
ผู้เขียนขอจบการนำเสนอซีรีส์สั้น “อินโฟกราฟฟิกที่ดี” แต่เพียงเท่านี้ อย่าลืมว่า ข้อมูลคือหัวใจ แต่ต้องใช้กราฟให้เป็น, สื่อให้เห็นความหมาย และอย่าตายน้ำตื้นกับสถิติ!